About me
I am a CNRS researcher at the Lagrange laboratory at the Côte d'Azur Observatory in Nice. My main research interests are the dynamical evolution of planetary systems, from their formation to their observation. I have studied the long-term stability of planetary systems both numerically and analytically. I also work on untangling the history of exoplanetary systems to constrain their formation and current configuration.
I completed my Ph.D. in June 2019 at the Ephemeris and Celestial Mechanics Institute (IMCCE) of the Paris Observatory under the supervision of Jacques Laskar and Gwenaël Boué. I mainly worked on the development of simple criteria to determine the stability of exoplanetary systems. In 2019, I joined as a postdoc the planet formation group of Anders Johansen at Lund University and then at the Globe Institute in Copenhagen. I joined the Côte d'Azur Observatory in 2023.
Research Interests
Selected works
The path to instability in compact multiplanetary systems
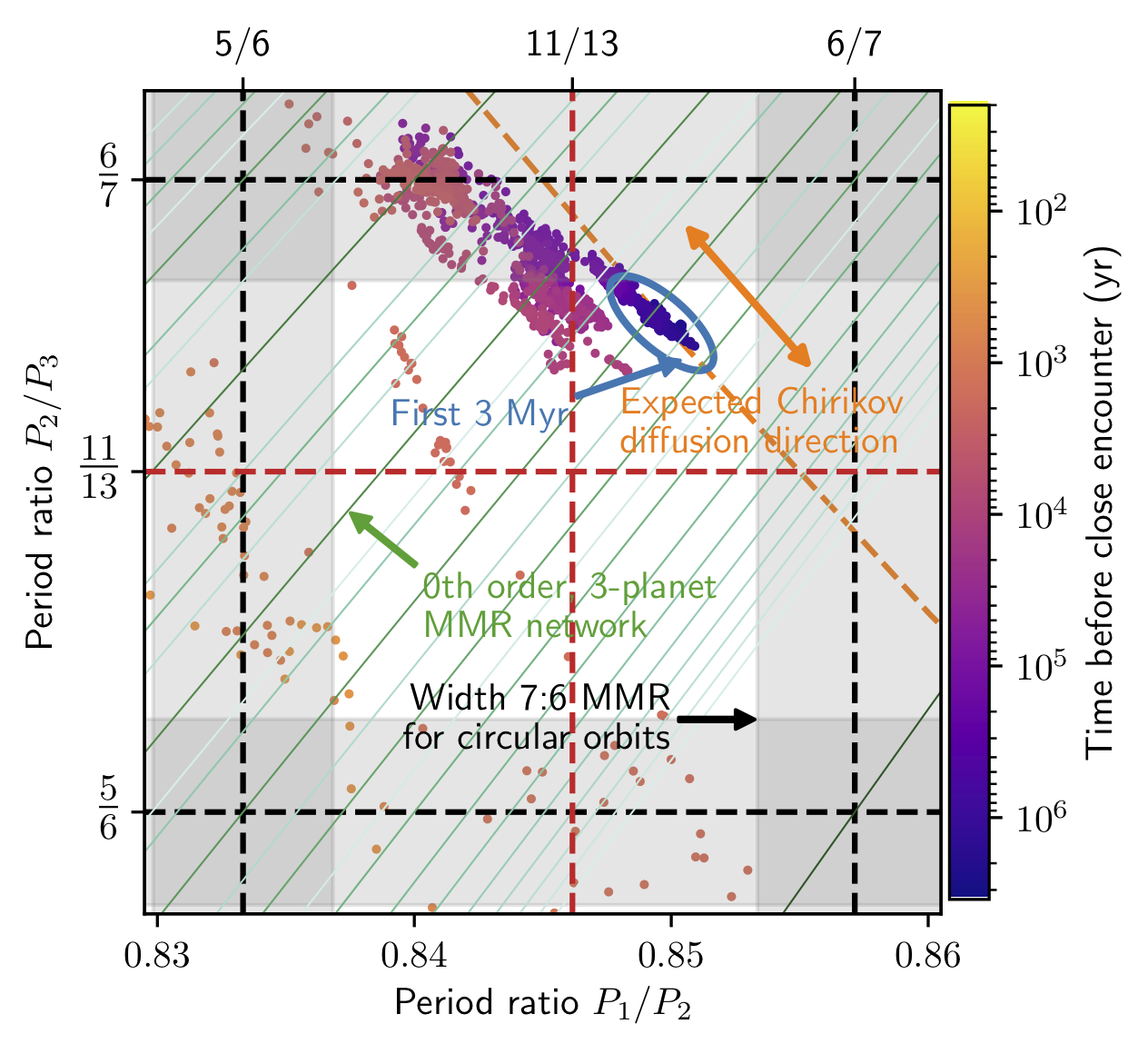Three or more compact planetary systems can become unstable on timescales of up to billions of years.
Predicting their stability is challenging and numerically expensive due to the chaotic dynamics, and, until now, there has been no theoretical understanding of the nature of the mechanism driving the instability.
Based on numerical simulations, it had been postulated that the system's survival time follows an exponential trend in the planet orbital separation measured in units of Hill radii.
Contrary to a constant diffusion process, planetary systems seem to remain dynamically quiescent for most of their lifetimes prior to a very short unstable phase.
In this work, I studied a two-phase mechanism in which the slow chaotic diffusion due to the overlap of three-body resonances dominates the instability timescale prior to a rapid scattering phase triggered by the crossing of a two-planet mean motion resonance.
I obtained an analytical estimate of the survival time that is consistent with numerical simulations over four orders of magnitude for the planet-to-star mass ratio, and six to eight orders of magnitude for the instability time.
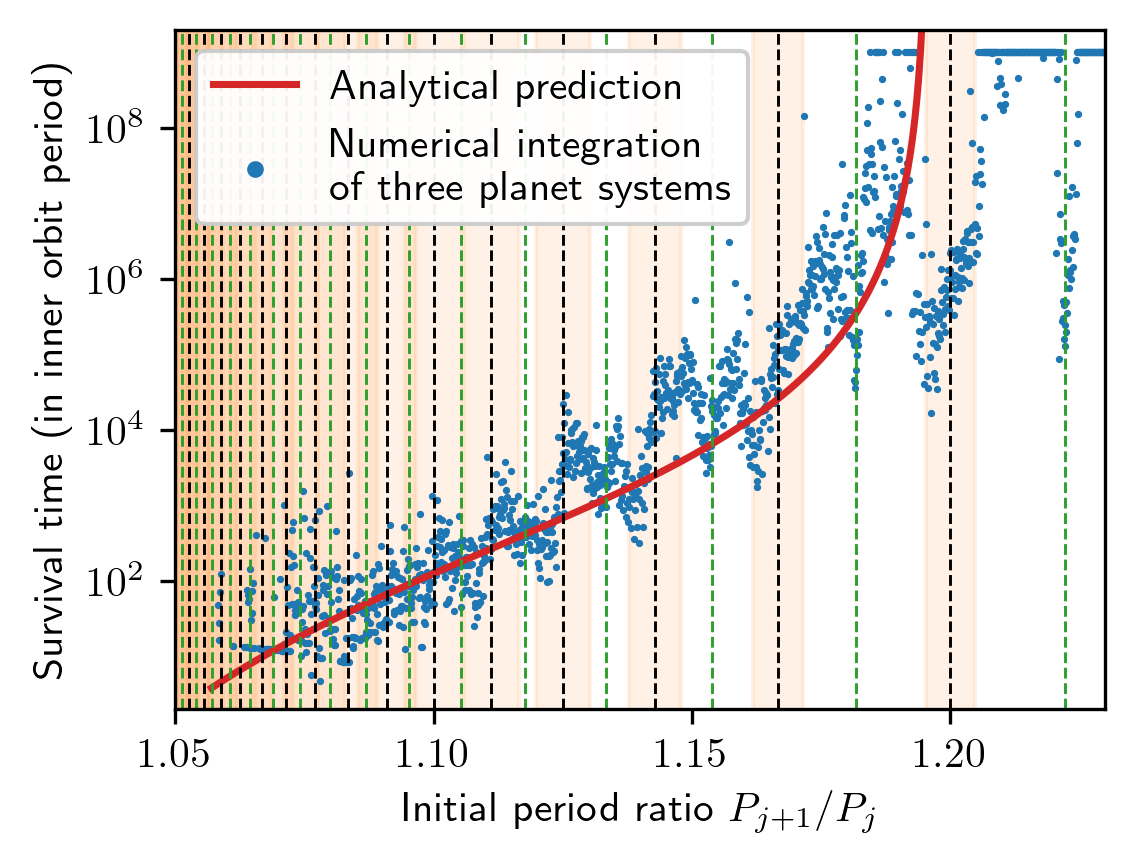I also confirmed that measuring the orbital spacing in terms of Hill radii is not suitable and that the correct spacing unit scales have a flatter dependency in the planet mass.
My model reproduces the observation that the survival time increases beyond a certain spacing since the three-planet resonances do not overlap.
A Python module that give the instability time scale can be found on GitHub.
AMD-stability and the classification of planetary systems
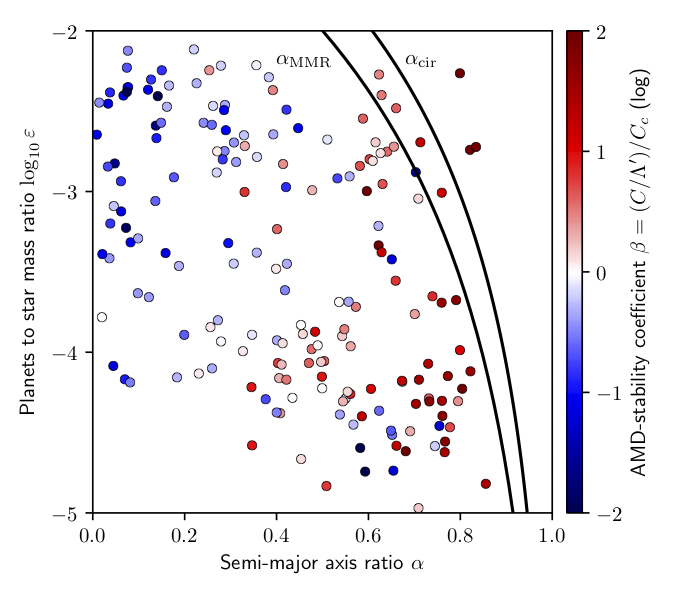The AMD or Angular Momentum Deficit (AMD) is a quantity that measures the dynamical excitment of a planetary system.
A large AMD means that planet orbit may cross, leading to the destruction of the planetary system.
I used it to classify the exoplanetary systems into two categories: the AMD-stable ones that will remain
stable over their lifetime because their AMD is too low to allow for collision and the AMD-unstable were
the AMD alone cannot ensure the stability of the system and that should be studied in more details.
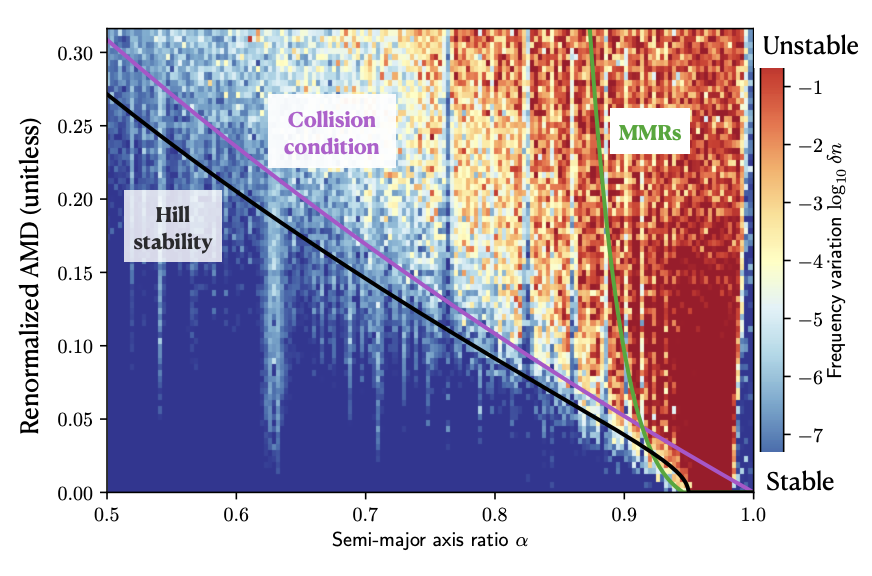An AMD-stability calculator is available on exoplanet.eu for selected systems.
My works with J. Laskar and G. Boué on the AMD-stability are published in the articles: